Funções progressimais Graceli.

Seja inicialmente f uma função contínua num intervalo [a,b] e tal que a função se forma a partir de progressão infinitésimas das distâncias para todo  .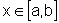

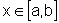 E que todo resultado representa a distância entre o eixo x da gráfico f.

Ou seja, temos um sistema infinitésimo para se encontrar resultados e curvas, sem usar derivadas, ou mesmo integrais.

1]F [x] = 1/ p.=

2]F[x] = 1 / p [ pP]=

3]F[x] = 1 / p2/d=

4]F[x] = 1 / p [ pP] + [p2/d ]=

Ou para uma função com alternância.

5] F[x] = 1 / p [ pP] + [p2/d ] [ a, x, b, p, 0,[p/pp]=

P = progressao.

P2/ d = produto e divisor.

A = alternância.

6] μ ΔF [x] = 1/ p.=

7]μ ΔF[x] = 1 / p [ pP]=

8]μ ΔF[x] = 1 / p2/d=

89]μ ΔF[x] = 1 / p [ pP] + [p2/d ]=

Ou para uma função com alternância.

10]μ ΔF[x] = 1 / p [ pP] + [p2/d ] [ a, x, b, p, 0,[p/pp]=

μ Δ = medial + variável .